Mathematics Project

Class:10 Date of submission:07/07/09

_____________________________________________________________

General Instructions:

- The project should be hand written

- Credit will be given to original and creative use of material/pictures/drawings/methods of illustrating

- The project must be presented in a neatly bound simple folder.

- Your last page should be

Name: Class

Roll No.

Assessment of the project work:

Identification and statement of project

Design of project

Procedure adopted

Write up of project

Interpretation of result

Total

Any one of the following projects may be chosen

A) Linear Equations

Project Assignment

Think of a question that asks about a cause and effect relationship between two measurable quantities. (eg.. does fingernail length affect typing speed?)

1. Write two different "how does _____ affect _____" questions.

2. Select the question that makes the most sense to you and explain why you have chosen it.

3. Write a hypothesis to answer your question.

4. Graph your data using appropriate choices of scales and axis.

5. In pencil, draw your "best" line.

6. Find the equation of your line.

Respond to the following questions

7. What do the variables in your equation represent? What does the equation represent?

8. Was your data positively correlated, negatively correlated or neither? Give possible explanations for the relationships or absence of relationships that you see in the data.

9. Use your equation to predict two data points not represented by the data. How good do you think these estimates are? why?

10. What information does the slope indicate?

Present your findings in a 3-4 pages handwritten report. Graph must be included.

B) Integer trains

You can use rods of integer sizes to build "trains" that all share a common length. A "train of length 5" is a row of rods whose combined length is 5. Here are some examples:

Notice that the 1-2-2 train and the 2-1-2 train contain the same rods but are listed separately. If you use identical rods in a different order, this is a separate train.

· How many trains of length 5 are there?

· Repeat for length 6

· Repeat for length 7

· Come up with a formula for the number of trains of length n. (Assume you have rods of every possible integer length available.) Prove that your formula is correct.

· Come up with an algorithm that will generate all the trains of length n.

· Create trains of lengths 6,7. Record any findings, conclusions in 3-4 pages of handwritten work.

C) Area of an Arbelos

Objective

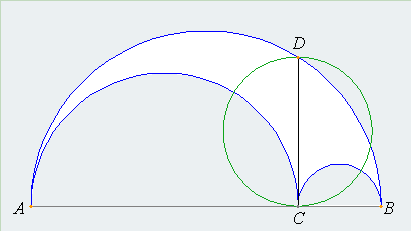
Objective: Prove that the area of the arbelos (white shaded region) is equal to the area of circle CD.

What is an arbelos?

The arbelos is the white region in the figure, bounded by three semicircles.

The diameters of the three semicircles are all on the same line segment, AB, and each semicircle is tangent to the other two. The arbelos has been studied by mathematicians since ancient times, and was named, apparently, for its resemblance to the shape of a round knife (called an arbelos) used by leatherworkers in ancient times.

An interesting property of the arbelos is that its area is equal to the area of the circle with diameter CD.

CD is along the line tangent to semicircles AC and BC (CD is thus perpendicular to AB). C is the point of tangency, and D is the point of intersection with semicircle AB.

Can you prove that the area of circle CD equals the area of the arbelos?

To do this project, you should do research that enables you to use the following terms and concepts:

• right triangles,
• circumscribing a circle about a triangle,
• similar triangles,
• area of a circle,
• Tangents are perpendicular to radii at the point of contact.

Materials and Equipment

For the proof, you'll need :

• pencil,
• paper,
• compass, and
• straight edge.

Experimental Procedure

1. Do your background research,
2. Organize your known facts, and
3. Spend some time thinking about the problem and you should be able to come up with the proof.
4. Present your findings in a 3-4 pages handwritten report.

D) Perimeters of Semi Circles

Objective

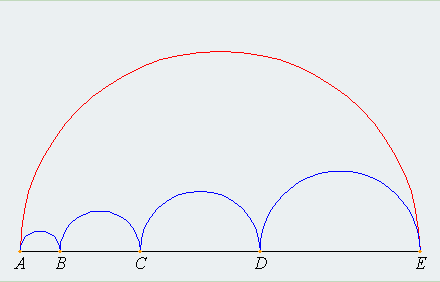
The objective of this project is to prove that the sum of the perimeters of the inscribed semicircles is equal to the perimeter of the outside semicircle.

Introduction

The figure below shows a semicircle (AE) with a series of smaller semicircles (AB, BC, CD, DE,) constructed inside it. As you can see, the sum of the diameters of the four smaller semicircles is equal to the diameter of the large semicircle. The area of the larger semicircle is clearly greater than the sum of the four smaller semicircles. What about the perimeter?

Your goal is to prove that the sum of the perimeters of the inscribed semicircles is equal to the perimeter of the outside semicircle.

Materials and Equipment

• For the proof, you'll need :
• pencil,
• paper,
• compass, and
• straight edge.
• Here's a suggestion for your display: in addition to your background research and your proof, you can make a model of the Figure with colored paper. Use a compass and straightedge to construct the semicircles. Cut pieces of string or yarn equal to the arc-lengths of the semicircles. You can use these to demonstrate that the perimeter lengths are indeed equal. Repeat for 3 different measurements of semi circles.

Experimental Procedure

1. Do your background research,
2. Organize your known facts,
3. Perform the experiments for 3 different semi circles
4. Tabulate your findings
5. Mathematically prove the result
6. Present your work in 3-4 handwritten pages.

E) Golden Ratio

In Mathematics and the Arts, two quantities are in the golden ratio if the ratio between the sum of those quantities and the larger one is the same as the ratio between the larger one and the smaller. The golden ratio is approximately 1.6180339887.

Eg 1, 1, 2, 3, 5, 8, 13, 21, 34, . . .

Let us consider 5, 8

5 + 8 = 13

13 8 = 1.6 approx.

8 5 = 1.6

This sequence of numbers is known as the Fibonacci sequence

Let's build an approximation of the golden rectangle using square grid paper.. At each step we will calculate the ratio of length to width. Remember the Golden Ratio is approximately 1.61803.

Step 1:  Start with a square 1 by 1.

Ratio

Step 2:  Add another 1 by 1 square.

Ratio

Step 3:  Add a 2 X 2 square.

Ratio

Step 4:  Add a 3 X 3 square.

Ratio

Step 5:  Add a 5 X 5 square.

Ratio

Step 6:  It's Your Turn! Build the next approximation on square grid paper .

Then observe the pattern and answer the following:

• Length_n =

Top of Form

• Length_n + width_n =

Top of Form

• The lengths of the various rectangles are 1, 2, 3, 5,..., Notice that each term is found by adding the 2 previous ones, the sequence known as the -----------

Top of Form

• Every step of the rectangle will produce a ratio closer and closer to the golden ratio of approximately

Top of Form

Which things around you are made in the golden ratio?

Measure the following with a centimeter measuring tape or stick. (Round measurements to the nearest .5 cm.) Then rank the items from closest (1) to the golden ratio to least close (4).

Rank

Item Measured	Length(cm)	Width(cm)	Ratio(L:W)
TV screen
Calculator
Math Textbook
Notebook paper
Rs 100 Bill

Find an item that has a ratio even closer to the golden ratio. List its dimensions and ratio below.

Item Measured

Length(cm)

Width(cm)

Ratio(L:W)

Challenge Problem

Take an 8 1/2 X 11 inch sheet of paper. Measure and make a golden rectangle by making one straight cut. Give the dimensions of all possible golden rectangles you could cut from

this sheet of paper

.

F) Fibonacci numbers and the Golden Number

If we take the ratio of two successive numbers in Fibonacci's series, (1, 1, 2, 3, 5, 8, 13, ..) and we divide each by the number before it, we will find the following series of numbers:

¹/₁ = 1,   ²/₁ = 2,   ³/₂ = 1·5,   ⁵/₃ = 1·666...,   ⁸/₅ = 1·6,   ¹³/₈ = 1·625,   ²¹/₁₃ = 1·61538...

It is easier to see what is happening if we plot the ratios on a graph:

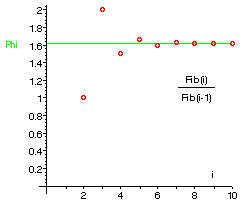
The ratio seems to be settling down to a particular value, which we call the golden ratio or the golden number. It has a value of approximately 1·618034 , although we shall find an even more accurate value .

Experiment :

What happens if we take the ratios the other way round i.e. we divide each number by the one following it: 1/1, 1/2, 2/3, 3/5, 5/8, 8/13, ..?
Use your calculator and perhaps plot a graph of these ratios and see if anything similar is happening compared with the graph above.
You'll have spotted a fundamental property of this ratio when you find the limiting value of the new series!

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 ..More..

The golden ratio 1·618034 is also called the golden section or the golden mean or just the golden number. It is often represented by a Greek letter Phi . The closely related value which we write as phi with a small "p" is just the decimal part of Phi, namely 0·618034.

Fibonacci Rectangles and Shell Spirals

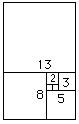We can make another picture showing the Fibonacci numbers 1,1,2,3,5,8,13,21,.. if we start with two small squares of size 1 next to each other. On top of both of these draw a square of size 2 (=1+1).

We can now draw a new square - touching both a unit square and the latest square of side 2 - so having sides 3 units long; and then another touching both the 2-square and the 3-square (which has sides of 5 units). We can continue adding squares around the picture, each new square having a side which is as long as the sum of the latest two square's sides. This set of rectangles whose sides are two successive Fibonacci numbers in length and which are composed of squares with sides which are Fibonacci numbers, we will call the Fibonacci Rectangles.

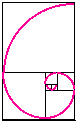Here is a spiral drawn in the squares, a quarter of a circle in each square. The spiral is not a true mathematical spiral (since it is made up of fragments which are parts of circles and does not go on getting smaller and smaller) but it is a good approximation to a kind of spiral that does appear often in nature. Such spirals are seen in the shape of shells of snails and sea shells and, as we see later, in the arrangement of seeds on flowering plants too. The spiral-in-the-squares makes a line from the centre of the spiral increase by a factor of the golden number in each square. So points on the spiral are 1.618 times as far from the centre after a quarter-turn. In a whole turn the points on a radius out from the centre are 1.618⁴ = 6.854 times further out than when the curve last crossed the same radial line.

Cundy and Rollett (Mathematical Models, second edition 1961, page 70) say that this spiral occurs in snail-shells and flower-heads referring to D'Arcy Thompson's On Growth and Form probably meaning chapter 6 "The Equiangular Spiral". Here Thompson is talking about a class of spiral with a constant expansion factor along a central line and not just shells with a Phi expansion factor.

Below are images of cross-sections of a Nautilus sea shell. They show the spiral curve of the shell and the internal chambers that the animal using it adds on as it grows. The chambers provide buoyancy in the water. Click on the picture to enlarge it in a new window. Draw a line from the centre out in any direction and find two places where the shell crosses it so that the shell spiral has gone round just once between them. The outer crossing point will be about 1.6 times as far from the centre as the next inner point on the line where the shell crosses it. This shows that the shell has grown by a factor of the golden ratio in one turn.

Bottom of Form